| 3 petals | 5 petals | 8 petals | 13 petals | 21 petals |
|---|---|---|---|---|
 |
 |
 |
 |
 |
Math is at the heart of many of the patterns we see in nature. Here's an interesting example called the Fibonacci series, named after an Italian mathematician of the Midde Ages, though the Greeks clearly knew all about it much earlier, as evidenced in the design of classical architecture such as the Parthenon. One common natural example is the number of petals on flowers, though of course there are exceptions.
| The series | The ratio | |||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | + | 1 | = | 1 | 1 | / | 0 | = | ? | |||||||||||||||
| 1 | + | 1 | = | 2 | 1 | / | 1 | = | 1 | |||||||||||||||
| 1 | + | 2 | = | 3 | 2 | / | 1 | = | 2 | |||||||||||||||
| 2 | + | 3 | = | 5 | 3 | / | 2 | = | 1.5 | |||||||||||||||
| 3 | + | 5 | = | 8 | 5 | / | 3 | = | 1.67 | |||||||||||||||
| 5 | + | 8 | = | 13 | 8 | / | 5 | = | 1.6 | |||||||||||||||
| 8 | + | 13 | = | 21 | 13 | / | 8 | = | 1.625 | |||||||||||||||
| 13 | + | 21 | = | 34 | 21 | / | 13 | = | 1.615 | |||||||||||||||
| and so on... | ||||||||||||||||||||||||
If we extend the series out indefinitely, the ratio approaches ~1.618:1, a constant we call phi, that is represented by the greek letter φ
| 3 petals | 5 petals | 8 petals | 13 petals | 21 petals |
|---|---|---|---|---|
 |
 |
 |
 |
 |
Video: Watch the following video for a nice explanation. While the presenter gets a bit carried away with some magical thinking, I like her enthusiasm.
The Golden Ratio
Activity: Get a pineapple and a box of colored push pins. As shown in the video above, put alike colored push pins into each cell of the pineapple, following the whorls, with a different color for each line. Take a picture of the pattern that emerges.
The Golden Spiral is a geometric way to represent the Fibonacci series and is represented in nature, if not always perfectly, in pine cones, nautilus and snail shells, pineapples, and more.
| Pineapple | Succulent | Pine Cone | Nautilus Shell | Sunflower |
|---|---|---|---|---|
 |
 |
 |
 |
 |
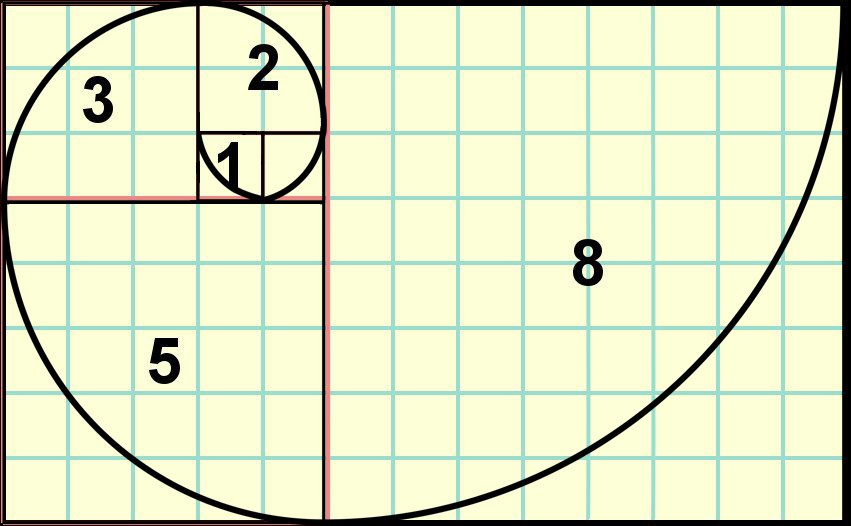
To draw the golden spiral, all you need is a compass and some graph paper or a ruler.
Watch this video to see how.
Modeling with Excel: Download this Excel file to create spirals like the Golden Spiral.
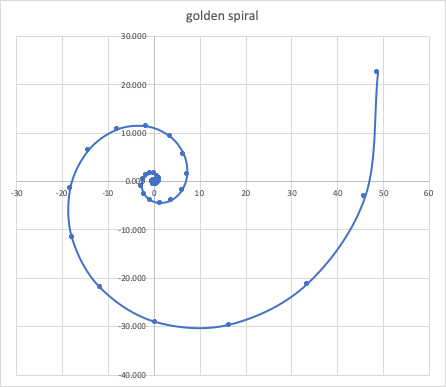

Explore how modifying the variables affects the curves.
Further reading:
https://www.nationalgeographic.org/media/golden-ratio/
http://www.maths.surrey.ac.uk/hosted-sites/R.Knott/Fibonacci/phi2DGeomTrig.html
https://www.youtube.com/watch?v=IGJeGOw8TzQ