Population Growth
Density-independent growth: At times, populations
invade new habitats that contain abundant resources. For a while at
least, these populations can grow rapidly because the initial number
of individuals is small and there is no competition for resources. This is called
density-independent growth because the density of individuals does
not have any effect on future growth. As you can imagine, this cannot
continue indefinitely. The first person to mathematically describe a population's potential to reproduce was Thomas Malthus, and his writings would influence the ideas of Charles Darwin.
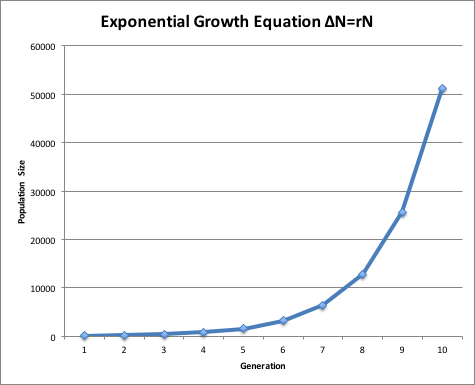
Take the equation below and run through 10 generations. Start with
an initial population size (Ni) of 100, and use a constant growth rate (r) of
1. (A growth rate of 0 indicates no reproduction, a value of 1 means doubling, higher values would yield more rapid population increases.) ΔN is the change in number. Nf
is the final number, after reproduction has occured, and is calculated as the initial number, Ni plus the change in number, ΔN. In generation 2, Nf becomes the new Ni and we run through the equation again. This kind of growth is called "exponential" and is fairly typical of bacterial cultures in fresh medium. Bacteria divide by binary fission (one becomes two) so the value of 2 for a growth rate is realistic. Graph your results.
ΔN = r Ni
Nf = Ni + ΔN
Density-dependent growth: In a population that is already
established, resources begin to become scarce, and competition starts
to play a role. We refer to the maximum number of individuals that a
habitat can sustain as the carrying capacity of that
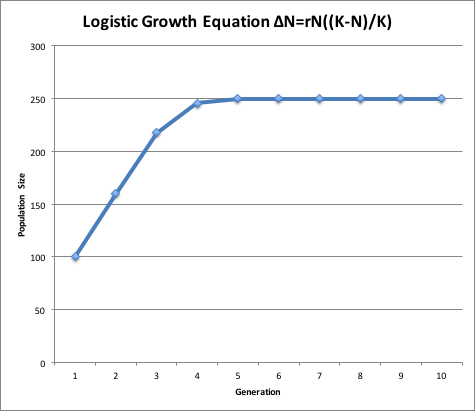
population. If a population overshoots its carrying capacity by too much, nobody gets enough resources and the population can crash to zero. If the population approaches its carrying capacity more gradually, these limiting factors, such as food, nesting sites, mates, etc. tend to regulate further growth and the population stabilizes. The "logistic equation" models this kind of population growth.
ΔN = r Ni ((K-Ni)/K)
Nf = Ni + ΔN
Compare the exponential and logistic growth equations. The rN part is the same, but the logistic equation has another term, (K-N)/K which puts the brakes on growth as N approaches or exceeds K.
Take the equation above and again run through 10 generations.
Start with an initial population size (Ni) of 100. Again, use a constant growth rate
(r) of 2. K is the carrying capacity of the population, which we will set at 500.
Graph your results.
Download the Excel file  to play around with the growth rates, initial population sizes, carrying capacity and watch the graphs re-draw dynamically.
to play around with the growth rates, initial population sizes, carrying capacity and watch the graphs re-draw dynamically.
Take a look at World Population Growth among humans. Predicting population growth accurately depends on a variety of factors. Clearly nutrition and disease are two important factors that affect survival to reproductive age, but also the ratio of males to females in a population (because females are the limiting factor) and the age distribution of the population (because younger populations have higher reproductive rates) are important parameters. How do war, famine, and environmental degradation relate to population size? Consider China's one child policy to limit population growth, and the social practices that favor one gender over the other in some cultures.
Further Reading: http://www.nature.com/scitable/knowledge/library/how-populations-grow-the-exponential-and-logistic-13240157