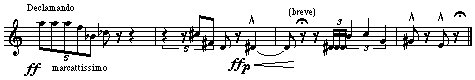
TEXTURE IN TWELVE-TONE COMPOSITION
Composers can use any known texture in twelve-tone composition. Conventional homophonic and polyphonic patterns are common in serial literature.
Certain features of twelve-tone composition affect other factors in a composition. For example, octave and enharmonic equivalence can produce extremely disjunct melody if no restriction is placed on the size of melodic intervals. The composer could distribute the notes in a row as fragments among several voices. The disjunct and fragmentary effect is sometimes called pointilism. A Klangfarbenmelodie (tone-color melody) is created if the fragments are moved systematically from color to color in the media.
The notes of a row can be distributed among two or more voices, in any octave, sounded one at a time or together as suggested below.
| 1 | 2 | 3 | 6 | 9 | 11 | 12 | |||
| 4 | 5 | 7 | 8 | 10 |
A row can appear in melodies, accompaniments, conversational flows, or counterpoint.
More than one row can sound at one time. Rows can overlap each other so that one row begins before another is completed, or one row can start on the last note of the previous row. Composers can combined forms so simultaneous rows periodically create twelve-tone aggregates (unordered collections), and they can select row forms that emphasize particular properties of the row. Composers seldom use all 48 possible forms in the twelve-by-twelve array in a single composition. Usually, a composer selects a few forms that have special relationships with each other.
The analyst should not stop at note counting but rather strive to recognize broader patterns of thought. In twelve-tone music, the composer's selection of particular forms of the row and how these are related to one another are particularly significant.
Take time to consider all the the systems that make up the composition such as texture, melody, and rhythm factors. At some point, view the composition as a whole organism, a system made up of a unique combination and interaction of subsystems.
Unaccompanied Melody
George Rochberg dramatically opened his second symphony with tutti octaves in the winds, brass, and percussion. He divided the row into three declamatory bursts.
Example 18: Symphony No. 2 mm1-4 George Rochberg
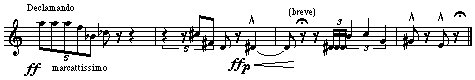
Accompanied Melody
In example, a row is assigned to a melody in the first violin. The other voices accompany the melody with a chord motif. Each chord motif consists of the complementary notes in the set (all but the three notes stated in the top voice). The twelve-tone aggregates formed by this technique are enclosed in dotted lines.
Example 19: String Quartet, no. 4, Op. 37, I Schoenberg
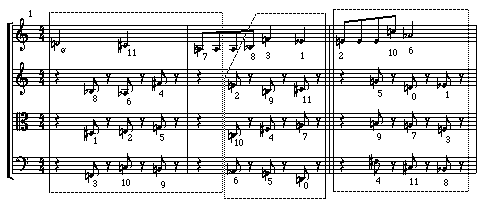
In example 20, the row is divided into distinct trichord cells. These cells progress through a series of rhythmic augmentations of the first cell. This process produces a cohesive conversation-like flow from timbre to timbre (see derived set, Example 13).
Example 20: Concerto for Nine Instruments, Op. 24, reduced score,
mm1-5 Webern 
Polyphony
Example 21 is a canon at the unison (TØ). The rhythmic offset is five quarter notes. The cells in the top voice are a rhythmic variation of the cells in the bottom voice. Rests were added to the top voice so that it would not overtake the lead voice. The PØ version of this row is in example 9.
Example 21: Contrapunctus Primus, mm1-4, N. 3, Quaderno Musicale di Annalibera Luigi Dallapiccola,
COMBINATORIALITY
Basis of Combinatorial Patterns, the Aggregate
An aggregate is an unordered collection of all twelve pitch classes. A twelve-tone aggregate is a harmony made up of all twelve pitch classes and can be presented melodically or harmonically in any combination. Aggregates can be created by sounding complementary parts of the same row together. In short, a row can accompany itself.
Complement
A set and its complement contain all twelve pitch classes. Any of the twelve pitch classes not included in a set are part of the complement. If a set contains four pitch classes, its complement will contain the remaining eight pitch classes.
Self-complementing Hexachords
As shown in example 22, some hexachords map onto their complements. A hexachord is self-complementing if the complement is the transposition or transposed inversion of the original and if it contains none of the original pitch classes. The hexachord and its complement are members of the same set class.
Example 22: Row from Ode to Napoleon, Op. 41 Schoenberg
Hexachordal Combinatoriality
Combinatoriality gives cohesiveness, consistency, and structure to a succession of ideas, longer span pitch modules, and to the large scale design of a composition. Hexachordal combinatoriality occurs if a hexachord combines with another form of itself to create an aggregate. This is possible with some but not all hexachords.
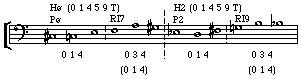
Example 23 shows how the hexachords of the PØ and I5 forms of a row combine to form twelve-tone aggregates. (I5 is the inversion at T5). The crisscross lines indicate that the linked hexachords contain identical pitch classes but in a different order.
Example 23: two combinatorial rows from works by Schoenberg
Piano Piece, Op. 33a String Quartet 4, Op. 37, 1937
|
|
|
Conditions of Hexachordal Combinatoriality
A hexachord is combinatorial if
1. The complement is produced by a transposition (maps onto its complement).
2. The complement is produced by an inversion (maps onto its complement).
3. A transposition produces the original collection of PCs (maps onto itself).
4. An inversion produces the original collection of PCs (maps onto itself).
Kinds of Combinatoriality
A hexachord that produces its complement under a transposition is prime combinatorial: the original hexachord and one of its transpositions combine to form an aggregate of all twelve pitch classes. Some hexachords are combinatorial under inversion, retrograde, or retrograde inversion (shown in example 24).
In the next example, Pø is the original row, and "n"represent an interval of transposition that varies from case to case. Disregard forms where n = ø (Rø always forms aggregates with Pø). H1 is the first and H2 the second hexachord of the original row.
Example 24: Kinds of combinatoriality
| Pø | H1 | H2 | Pø | H1 | H2 | |||
| prime combinatorial | Pn | H1 | H2 | inversion combinatorial | In | H1 | H2 |
| Pø | H1 | H2 | Pø | H1 | H2 | |||
| retrograde combinatorial | Rn | H2 | H1 | retrograde-inversion combinatorial | RIn | H2 | H1 |
|
The hexachords in the rows used by Schoenberg in Op. 33a and Op. 37 (see example 23) are inversion combinatorial at T5. |
All-Combinatorial Hexachords
Only a few hexachords are combinatorial in all forms. Six of the hexachord set classes are all-combinatorial. An all-combinatorial hexachord produces its complement in I, R, and RI forms under one or more transpositions.
|
Class |
The six all-combinatorial hexachords are presented in Table 1. • The first three hexachords first order classes produce complements under only one transposition and one inversion (number 1 is a chromatic hexachord, number 3 a diatonic hexachord) • The fourth hexachord is a second order class that produces complements under two transpositions and inversions • The fifth hexachord is a third order class that produces complements under three transpositions and inversions (consists of three m2 a major third apart) • The sixth hexachord is a fourth order class that produces complements under six transpositions and inversions (a whole tone hexachord) |
|
Column |
• The "Pitches in the Hexachord" column includes the six pitch classes of the hexachord written in normal form starting on C. • The "Set Class" column contains the prime forms of the hexachords. • "T6" indicates transposition interval; "at T3" indicates a pattern is repeated a minor third higher. • The "Trichord" column shows how each of hexachord is divided into two trichords of the same class. • If a hexachord is made up of recurring dyads of the same class, this is noted in the "comment" column along with the transposition level of the two recurrences of the dyad. The three hexachords that form traditional scale patterns are noted here. |
Schoenberg and Webern explored some of the potential of all-combinatorial hexachords in various works. The nature of these hexachords was investigated and described in a doctoral dissertation completed by Milton Babbitt in 1947 and subsequently developed in the compositions of Babbitt and his followers. Both Babbitt and Allen Forte have made a sizable contribution to the classification and description of all set classes.
Table 1: Six all-combinatorial hexachords (each produces complementary hexachords in all forms)
| Pitches in the Hexachord | Set Class | Complement | Trichords | Comments | ||||||
| 1. | C |
C |
D |
D |
E | F | (0 1 2 3 4 5) | T6, I11 | (0 1 2) at T3 | chromatic (0 1) at T2 and T4 |
| 2. | C | D |
D |
E | F | G | (0 2 3 4 5 7) | T6, I1 | 0 2 3 at Ø (0 1 3) at T4* | |
| 3. | C | D | E | F | G | A | (0 2 4 5 7 9) | T6, I3 | (0 2 4) at T5 | diatonic |
| 4. | C |
C |
D |
F |
G |
G |
(0 1 2 6 7 8) | T3,9 I5,11 | (0 1 2) at T6 | |
| 5. | C |
C |
E | F |
G |
A | (0 1 4 5 8 9) | T2,6,10 I3,7,11 | (0 1 4) at Ø 0 3 4 at T5* | (0 1) at T4 and T8 |
| 6. | C | D | E |
F |
G |
A |
(0 2 4 6 8 10) | T1,3,5,7,9,11 I1,3,5,7,9,11 | (0 2 4) at T6 | whole-tone (0 2) at T4 and T8 |
*note the occurrence of both normal and prime forms of a trichord in the second and fifth hexachords.
A Case Study of Duet by Milton Babbitt
Duet, a composition for piano by Milton Babbitt, is discussed in the next five examples. This series of examples illustrates an approach to the analysis of a whole twelve-tone work.
An overview of the Duet reveals that the texture of the work is non-imitative polyphony. No deliberate or systematic repetition of motives is evident, but a certain unity is achieved through the repetition of certain rhythm ideas. Phrases are punctuated by rhythmic and contour closures. The row forms and the phrasing are not coordinated. The role of lead voice changes periodically.
Babbitt helped to develop and refine the concept of combinatoriality so one can approach one of his compositions with the expectation that it may contain combinatorial features. To confirm, see if the first hexachords in each voice combine to form an aggregate in example 25..
The first note played, A
,, is PCØ. Ha is the first hexachord of the row. Ha6
is the first hexachord at T6. A comparison of the first hexachords in
both voices of Duet indicates that the composer used a
combinatorial method. The hexachord in the bottom part (Ha) is repeated
in the top part at T6. HaØ and Ha6 are complements because they
form an aggregate of the twelve pitch classes.
The first nineteen measures of Duet are included in examples 25-28. Perform them non-stop.
Example 25: Duet mm. 1-3 Milton Babbitt
The second hexachords (Hb) in the two voices also form aggregates (second beat of m. 3 and ending on the downbeat of m. 6 in examples 25 and 26), further evidence of combinatorial method. Again, one hexachord is the transposition of the other at the tritone (T6). HbØ and Hb6 are complements because they also form an aggregate of all twelve pitch classes.
Construct a twelve-tone matrix (twelve by twelve array) based on the
PØ in the bottom voice of m. 1 (starts on A).
Example 26: Duet mm. 4-7
The RI5 and R6 forms of the row are presented at m. 6 (see examples 26 and 27). The I11 and RI11 forms of the row begin at the upbeat to m. 11.
Example 27: Duet mm. 8-11
The RIØ and I5 forms of the row begin at the upbeat to m. 15.
Example 28: Duet mm. 12-19
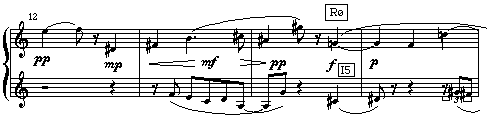
Synopsis of Duet
The row forms used in Duet were as follows (
= downbeat,
= upbeat).
| Location of row form |
of m. 1 |
after of m. 6 |
to m. 11 |
to m. 15 |
| Voice 1 | P6 | RI5 | I11 | RØ |
| Voice 2 | PØ | R6 | RI11 | I5 |
The hexachords in each voice always combine to form an aggregate
containing the twelve pitch classes. When placed in prime form, the
hexachords are all of class (0 2 4 5 7 9), the diatonic hexachord. As
illustrated in the first bars of Duet (mm. 1-3), this hexachord
maps onto its complement at T6. G A B C D E becomes
C D E F G A when transposed by the interval of a tritone.
The diatonic hexachord is one of six all-combinatorial hexachords identified by Babbitt (see Table 1). According to the table of all-combinatorial hexachords, this class is P, I, R, and RI combinatorial at one transposition level. This means that Ha and Hb form aggregates when paired in different row forms at certain transposition levels. The analysis suggests that use of combinatorial possibilities was part of Babbitt's plan for Duet. The second two hexachords of Voice 1 are R6 of the first two hexachords in reverse order. The second two hexachords of Voice 2 are I5 of the first two hexachords in reverse order.
Continuous repetition of one kind of hexachord adds unity to Duet. The combination of the hexachords yields a limited number of dyads. The interval sounds and the ensuing level of dissonance are regulated by the combinatorial relationships.
Tropes
Tropes are created by systematically shifting elements of a set each time the set is repeated. This technique is like the rotation of notes in subsets. As shown below, composers can rotate the notes of hexachords in trichord groups. The sample marked B1 is new basic order of the notes. B1 can be rotated to produce versions B2 and B3 (not shown). The trichords can be rotated in opposite directions in each hexachord to create even more possibilities.
Example 29: The production of tropes within hexachords
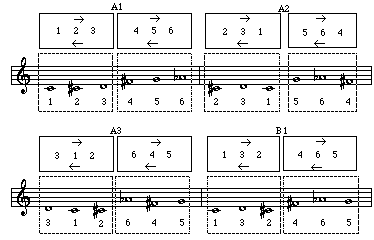
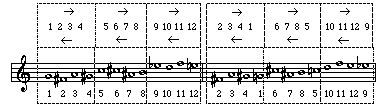
In a twelve-tone composition, a row can be made up of complementary hexachords each of which can be rotated to produce a series of tropes. This process can also be applied to a row divided into tetrachords. Example 30 shows a few of the tropes made possible by rotating the notes of tetrachords in a derived set.
Example 30: Tropes based on tetrachords.
Stravinsky used rotation of hexachords in several compositions, sometimes transposing each rotation to PCØ (see scores of Abraham and Isaac, Movements for Orchestra, The Flood, A Sermon, A Narrative, A Prayer for details on Stravinsky's use of tropes).
Krenek, Perle, and Hauer discussed tropes in their theoretical writings. See articles like Sets and Order Procedures" in Aspects of Twentieth Century Music by Gary Wittlich.
Serialization of other Factors
The works of Webern, Boulez, Krenek, Babbitt and others contain examples of serialized rhythm, articulation, dynamics, and register. Webern serialized more than one factor in his Variations for Piano, II, Op. 27; Symphony, Op. 21; Concerto for Nine Instruments, Op. 24; and String Quartet, Op. 28.
Other dimensions of a composition subject to serialization can include attack, timbre, time point, and textural density. Music in which several factors are serialized is called multi-serial music or total serialism.
Summary
Twelve-tone method is one of several important techniques developed in the twentieth century. Many prominent composers have tried the method at one time or another in their careers, and some have adopted the technique as a permanent feature of their style and method. Other composers do not use the twelve-tone method but may work with pitch and rhythm cells as sets. The serialists developed the idea of sets into a rigorous methodology.
The twelve-tone music of Arnold Schoenberg features rich orchestration, remarkable and unique colors, provocative subjects and expressions, and sonic drama. He continued to consider these factors throughout his career. They are as much a part of Schoenberg's musical thought as the twelve-tone method he developed.
Twelve-tone method may be an important part of writing a particular composition, but it does not eliminate the need to make artistic decisions about the timing of events, thematic rhythms, use and contrast of textural patterns and effects, or the use of media (voice; acoustic, electronic, invented instruments). When studying a twelve-tone composition, consider all the factors that go into the artistic product. Do not discount significant factors simply because they lie outside the control of the serial technique.
Serial method is a subject of considerable depth. The material presented on these pages is merely an introduction to the topic. Students can find many articles and chapters about serial study, some of which are suitable for graduate study. A large body of twelve-tone literature is available in scores and recordings.
Go to Terms and Problems, Part 2Back to Twelve Tone Composition, Part 1
