Inter-specific Competition
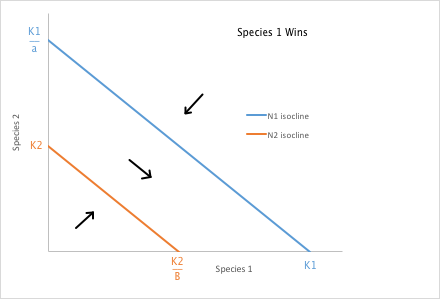
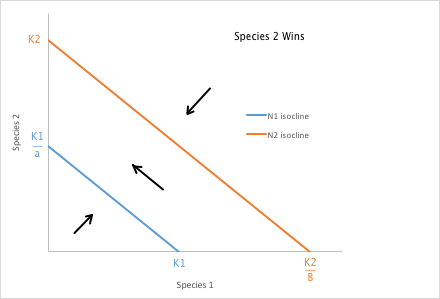
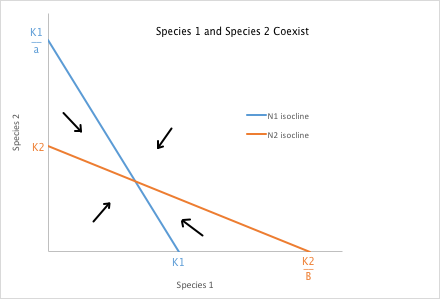
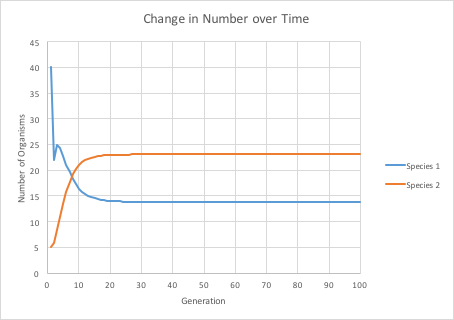
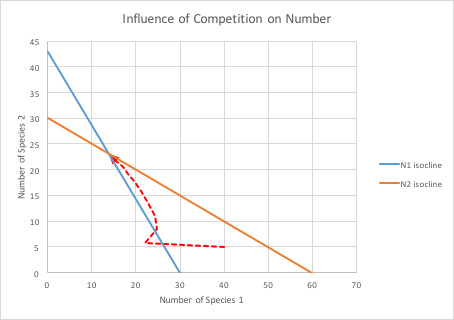
As we learned from the bird beak lab, inter-species competition for a finite resource can be quite intense, and can result in partitioning of a niche or local extinction of the less successful species. We can model these interactions mathematically. Remember the logistic growth equation? That's the starting point for these calculations. If there is no competition between two species, then they should grow in number until they reach the carrying capacity of the local environment. However, if a second species is interfering with the first, then the first species will be less successful and, depending on the degree of interference or inhibition, the first species might die out or stabilize at a lower number. It is also possible that the first species interferes with the second, so both species may be negatively affected by the competition with each other for a limited resource. Here, then, are the equations for Species 1 and Species 2. The new terms, αN2 and βN1 serve to reduce the number of the opposite species based on how badly the competing species inhibits the other (the α and β terms) multiplied by the number of individuals of the competing species. Note that if either the competition factor is zero or the number of competitors present is zero, this term drops out and the other species reaches its carrying capacity.
Species 1: ΔN1 = r1 N1 ((K1 - N1 - αN2 ) / K1) where α = negative effect of Species 2 on Species 1
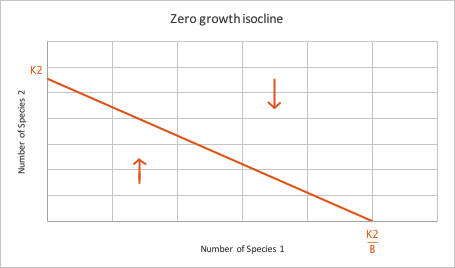
Species 2: ΔN2 = r2 N2 ((K2 - N2 - βN1 ) / K2) where β = negative effect of Species 1 on Species 2
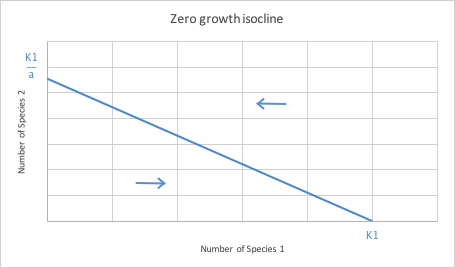
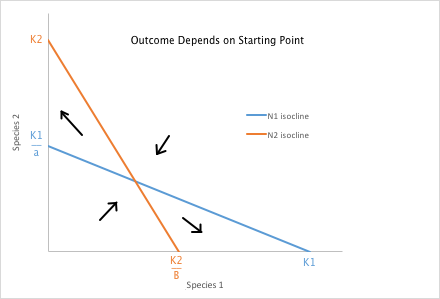
Species 1 Isocline: How can we figure out when a species will increase in number and when it will decrease? If Species 2 is not part of the picture (N2=0) there is no suppression due to competition, so the growth or decline of Species 1 is determined only by how many there are currently, and by the carrying capacity of Species 1. If there are more of Species 1 than the carrying capacity (N1>K1) then species 1 will decline. If there are fewer of species 1 than the carrying capacity (N1<K1) then species 1 will increase. If species 1 is at the carrying capacity (N1=K1) then there will be no change in number. On a graph of Species 1 vs Species 2, the carrying capacity of Species 1, K1 is the x-intercept of a line. But at what number of Species 2 is there zero growth of Species 1? We can solve for the y-intercept of our zero-growth line by plugging in a zero for N1 (where the number of Species 1 is not changing) and solving for N2
(K1 - N1 - αN2) = 0
K1- αN2 = 0
K1= αN2
K1/α = N2